Unlock The Secrets Of The Trapezoid Formula: Your Ultimate Guide
Table of Contents
- What Exactly is a Trapezoid?
- Why the Trapezoid Formula Matters?
- Unveiling the Trapezoid Area Formula
- Step-by-Step: Calculating the Area of a Trapezoid
- Beyond Area: The Trapezoid Perimeter Formula
- Special Types of Trapezoids
- Finding the Height of a Trapezoid: When It's Missing
- Mastering Trapezoid Formulas: Practical Examples & Worksheets
What Exactly is a Trapezoid?
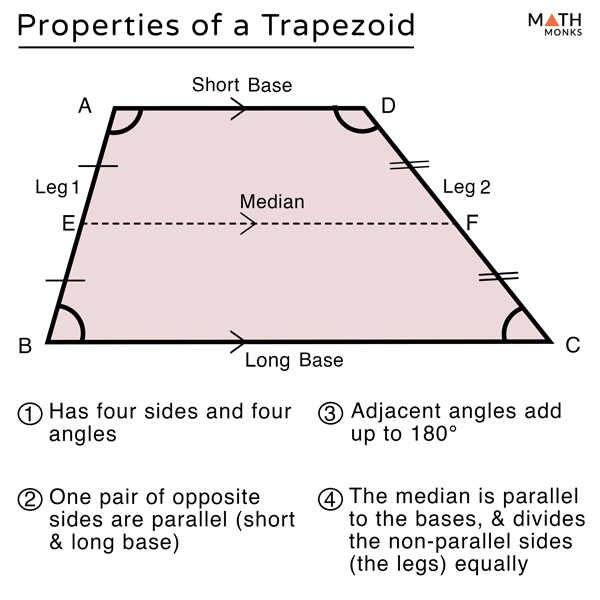
Before we dive into the trapezoid formula, let's establish a clear understanding of what a trapezoid is. In the realm of Euclidean geometry, a trapezoid (known as a trapezium in Britain and other parts of the world) is a convex quadrilateral. What does that mean? It's a flat, closed shape with four straight sides. The defining characteristic of a trapezoid is that it has at least one pair of parallel sides. These parallel sides are referred to as the "bases" of the trapezoid. The other two non-parallel sides are called "legs." The perpendicular distance between the two parallel bases is known as the "height" or "altitude" of the trapezoid. Imagine a rectangle, and then slice off its top portion at an angle – you're likely left with a trapezoid. This unique structure makes it distinct from other quadrilaterals like squares, rectangles, or parallelograms, which have two pairs of parallel sides. Understanding these fundamental properties is the first step toward mastering the trapezoid formula.Why the Trapezoid Formula Matters?
You might wonder, "Why do I need to know the trapezoid formula?" The truth is, trapezoids are everywhere, often without us even realizing it. From the architectural design of modern buildings, where sloped roofs or unique window shapes might be trapezoidal, to the engineering of bridges and road constructions, the principles of trapezoids are vital. Think about the cross-section of a canal or a dam, the shape of a lampshade, or even certain pieces of furniture – many of these incorporate trapezoidal forms. In practical applications, knowing the trapezoid formula allows engineers, architects, and designers to accurately calculate the area of surfaces, the volume of materials needed, or the dimensions for construction. For instance, if you're building a garden bed with sloped sides or designing a custom countertop, the ability to calculate the area of a trapezoid ensures precision and efficiency. It's not just about passing a math test; it's about equipping yourself with a tool that has real-world utility, making the trapezoid formula an indispensable part of your mathematical toolkit.Unveiling the Trapezoid Area Formula
The most frequently used trapezoid formula is for calculating its area. The area of a trapezoid represents the total space contained within its perimeter. Conceptually, the area of a trapezoid is basically the average width times the altitude (or height). This intuitive understanding helps in remembering the formula. The standard trapezoid area formula is expressed as: **A = ½ (b₁ + b₂) h** Where: * **A** is the area of the trapezoid. * **b₁** is the length of the first base (one of the parallel sides). * **b₂** is the length of the second base (the other parallel side). * **h** is the altitude (height), which is the perpendicular distance between the two bases. This formula essentially takes the average of the lengths of the two parallel bases and then multiplies it by the height. It's a straightforward yet powerful formula that unlocks the measurement of the space a trapezoid occupies.Deriving the Area Formula: A Visual Approach
Understanding where a formula comes from can deepen your comprehension and make it easier to recall. The trapezoid area formula, A = ½ (b₁ + b₂) h, can be beautifully derived using simpler geometric shapes like rectangles and triangles. Imagine a trapezoid. You can always divide a trapezoid into a rectangle and one or two triangles. For example, if you draw perpendicular lines from the ends of the shorter base down to the longer base, you'll form a rectangle in the middle and two right-angled triangles on either side (unless it's a right trapezoid, in which case it's one rectangle and one triangle). Alternatively, consider making a copy of the trapezoid, rotating it 180 degrees, and placing it next to the original so that their non-parallel sides align. What you've created is a parallelogram! The base of this new parallelogram would be (b₁ + b₂), and its height would be 'h'. The area of a parallelogram is simply base × height, so its area would be (b₁ + b₂)h. Since this parallelogram is made up of two identical trapezoids, the area of one trapezoid must be half of the parallelogram's area. Hence, A = ½ (b₁ + b₂)h. This visual derivation reinforces the logic behind the trapezoid formula.Step-by-Step: Calculating the Area of a Trapezoid
Calculating the area of a trapezoid using the trapezoid formula is a simple process once you have the necessary measurements. Here's a clear, step-by-step guide: 1. **Identify the Bases (b₁ and b₂):** The first step is to find the lengths of the two parallel sides. These are your b₁ and b₂ values. It doesn't matter which parallel side you label b₁ or b₂, as addition is commutative (b₁ + b₂ is the same as b₂ + b₁). 2. **Determine the Height (h):** Next, measure or identify the perpendicular distance between these two parallel bases. This is your 'h' value. Remember, the height must be perpendicular to the bases, not the length of a slanted leg. 3. **Substitute Values into the Formula:** Once you have b₁, b₂, and h, plug these values into the trapezoid area formula: A = ½ (b₁ + b₂) h. 4. **Perform the Calculation:** * First, add the lengths of the two bases: (b₁ + b₂). * Then, multiply that sum by the height: (b₁ + b₂) × h. * Finally, divide the result by 2 (or multiply by ½): [(b₁ + b₂) × h] / 2. **Example:** Let's say a trapezoid has bases of 6 cm and 10 cm, and its height is 4 cm. * b₁ = 6 cm * b₂ = 10 cm * h = 4 cm Using the trapezoid formula: A = ½ (6 + 10) × 4 A = ½ (16) × 4 A = 8 × 4 A = 32 cm² Always remember to include the appropriate square units (e.g., cm², m², ft²) when stating the area.Beyond Area: The Trapezoid Perimeter Formula
While the area is often the focus, understanding the trapezoid perimeter formula is equally important. The perimeter of any geometric figure is simply the total distance around its outer boundary. For a trapezoid, this means adding up the lengths of all four of its sides. Let's denote the four sides of a trapezoid as a, b, c, and d. The two parallel sides are typically referred to as the bases (let's say 'a' and 'b' are the bases), and the other two non-parallel sides are the legs (let's say 'c' and 'd'). The trapezoid perimeter formula is straightforward: **P = a + b + c + d** Where: * **P** is the perimeter of the trapezoid. * **a, b, c, d** are the lengths of the four sides. Unlike the area formula, the height is not directly used in calculating the perimeter unless you need to find the length of a missing side using the Pythagorean theorem in a right trapezoid or by constructing right triangles within a general trapezoid. Finding the perimeter of a trapezoid is simply about summing the lengths of all its sides, which makes it one of the two basic trapezoid formulas. **Example:** Consider a trapezoid with parallel bases of 7 inches and 12 inches, and legs measuring 5 inches and 6 inches. * a = 7 inches * b = 12 inches * c = 5 inches * d = 6 inches Using the trapezoid perimeter formula: P = 7 + 12 + 5 + 6 P = 30 inches The perimeter is expressed in linear units (e.g., cm, m, inches).Special Types of Trapezoids
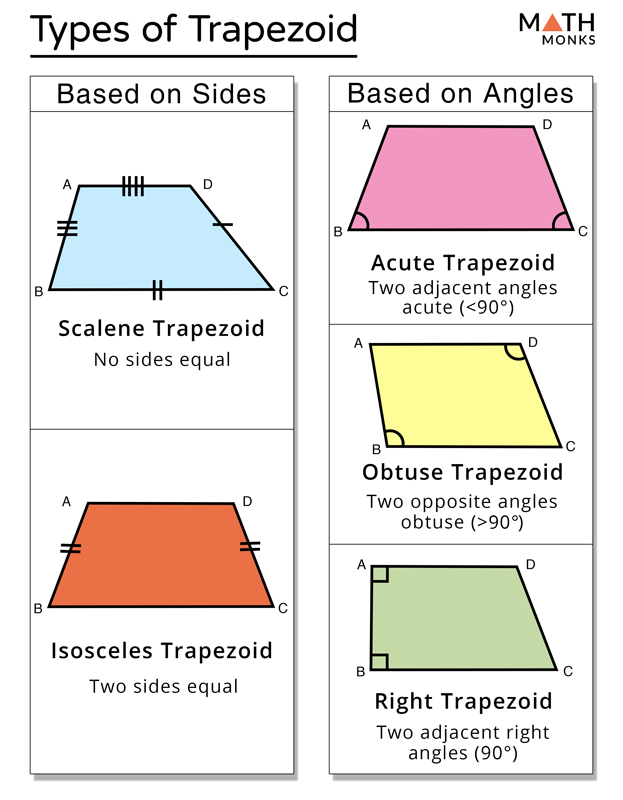
While the general trapezoid formula applies to all trapezoids, some specific types have additional properties that can simplify calculations or offer unique insights. Understanding these special quadrangles adds another layer to your mastery of trapezoids.Isosceles Trapezoids: Symmetry and Simplicity
An isosceles trapezoid is a trapezoid where the non-parallel sides (legs) are equal in length. This equality introduces a beautiful symmetry. In an isosceles trapezoid: * The base angles are equal (angles at each end of a base are congruent). * The diagonals are equal in length. * It has a line of symmetry that bisects the parallel bases. These properties can be useful when solving problems, as they often provide additional information that might be missing in a general trapezoid. For example, if you know one base angle, you know the other base angle on the same base. When dealing with an isosceles trapezoid, the trapezoid formula for area remains the same, but finding missing side lengths or angles might be easier due to its symmetry.Right Trapezoids: The Perpendicular Advantage
A right trapezoid (also known as a right-angled trapezoid) is a trapezoid that has at least one pair of right angles. This means that one of its non-parallel sides is perpendicular to both parallel bases. Essentially, one of the legs acts as the height of the trapezoid. This characteristic simplifies certain calculations. For instance, if you're given a right trapezoid, the length of its perpendicular leg is directly its height 'h'. This eliminates the need to calculate the height separately if that leg's length is known. The presence of a right angle also means you can often use the Pythagorean theorem to find missing side lengths if you form a right triangle by dropping a perpendicular from one vertex to the opposite base. The trapezoid formula for area and perimeter remains consistent, but the geometric properties of a right trapezoid often make finding the necessary values more straightforward.Finding the Height of a Trapezoid: When It's Missing
Sometimes, you might know the area of a trapezoid and the lengths of its bases, but the height is unknown. In such scenarios, you can rearrange the trapezoid formula for area to solve for the height. This is a common problem-solving technique in geometry.Calculating Height from Area: A Reverse Challenge
Let's start with the original trapezoid area formula: A = ½ (b₁ + b₂) h To find 'h', we need to isolate it. 1. Multiply both sides by 2: 2A = (b₁ + b₂) h 2. Divide both sides by (b₁ + b₂): h = 2A / (b₁ + b₂) So, the formula to find the height of a trapezoid given its area is: **h = 2A / (b₁ + b₂)** This inverse application of the trapezoid formula is incredibly useful. For example, if you have a plot of land shaped like a trapezoid and know its total area and the lengths of its parallel boundaries, you can easily determine the perpendicular distance between those boundaries. This demonstrates the versatility and practical power of the trapezoid formula in various problem-solving contexts. **Example:** A trapezoid has an area of 45 square meters. Its bases are 8 meters and 10 meters long. What is its height? * A = 45 m² * b₁ = 8 m * b₂ = 10 m Using the rearranged trapezoid formula for height: h = 2 × 45 / (8 + 10) h = 90 / 18 h = 5 meters The height of the trapezoid is 5 meters.Mastering Trapezoid Formulas: Practical Examples & Worksheets
The best way to truly master the trapezoid formula and its variations is through practice. Working through various examples and exercises solidifies your understanding and builds confidence. Here, we'll provide a few more examples and encourage you to seek out worksheets for continued practice. **Example 1: Finding the Area** A garden plot is shaped like a trapezoid with parallel sides measuring 15 feet and 25 feet. The perpendicular distance between these sides is 10 feet. Calculate the area of the garden. * b₁ = 15 ft * b₂ = 25 ft * h = 10 ft Using the trapezoid formula for area: A = ½ (b₁ + b₂) h A = ½ (15 + 25) × 10 A = ½ (40) × 10 A = 20 × 10 A = 200 square feet The garden plot has an area of 200 square feet. **Example 2: Finding the Perimeter** A decorative window frame is in the shape of a trapezoid. The top parallel side is 30 cm, the bottom parallel side is 50 cm, and the non-parallel sides are 25 cm and 28 cm. What is the perimeter of the window frame? * a = 30 cm * b = 50 cm * c = 25 cm * d = 28 cm Using the trapezoid perimeter formula: P = a + b + c + d P = 30 + 50 + 25 + 28 P = 133 cm The perimeter of the window frame is 133 cm. **Example 3: Finding a Missing Base (Advanced Application)** A trapezoidal field has an area of 1200 square meters and a height of 30 meters. One of its parallel sides measures 40 meters. What is the length of the other parallel side? Here, we'll use the area formula and solve for a base. A = ½ (b₁ + b₂) h 1200 = ½ (40 + b₂) × 30 Multiply both sides by 2: 2400 = (40 + b₂) × 30 Divide both sides by 30: 2400 / 30 = 40 + b₂ 80 = 40 + b₂ Subtract 40 from both sides: b₂ = 80 - 40 b₂ = 40 meters The length of the other parallel side is 40 meters. This particular trapezoid is actually a parallelogram, as both parallel sides are equal. These examples illustrate the versatility of the trapezoid formula. For further practice, look for online geometry worksheets or textbooks that provide various problems involving trapezoids. Solving problems where you need to find the area, perimeter, height, or even a missing base will significantly enhance your understanding and application skills. **In conclusion, the trapezoid formula, whether for area or perimeter, is a foundational concept in geometry with wide-ranging practical applications.** From understanding the basic definition of a trapezoid as a quadrilateral with one pair of parallel sides to deriving and applying its area formula (A = ½ (b₁ + b₂) h) and perimeter formula (P = a + b + c + d), you now possess a comprehensive understanding. We've explored how to calculate the area, how to find the height when given the area, and even touched upon special types of trapezoids that offer unique properties. The ability to accurately calculate the area of trapezoids is invaluable in fields like construction, design, and even everyday problem-solving. By grasping these formulas and their underlying principles, you're not just memorizing equations; you're developing a deeper appreciation for the logic and elegance of mathematics. Keep practicing, keep exploring, and let your newfound knowledge of the trapezoid formula empower you in your future endeavors. Do you have any challenging trapezoid problems you've encountered? Share them in the comments below! Or perhaps you have a unique real-world example of where you've seen a trapezoid in action? We'd love to hear your insights. If you found this article helpful, consider sharing it with others who might benefit from mastering the trapezoid formula. Explore our other geometry articles for more fascinating mathematical insights!- Bob Johnson Toyota
- Chris Isaak Songs
- Crossroads Bellevue
- Arrowhead Bmw
- Trice Funeral Home Obituaries
Trapezoid – Definition, Properties, Formulas & Examples

Trapezoid - Wikipedia
Trapezoid – Definition, Properties, Formulas & Examples